NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals are an educational aid for students to solve and learn simple and difficult problems. It includes a complete set of questions organised with an advanced level of difficulty, which provides students ample opportunity to apply their knowledge and skills. Get free NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals devised according to the latest update on CBSE Syllabus for 2023-24.
Download Exclusively Curated Chapter Notes for Class 9 Maths Chapter – 8 Quadrilaterals
Download Most Important Questions for Class 9 Maths Chapter – 8 Quadrilaterals
The NCERT Solutions will help the students to understand the concept of Quadrilaterals – mainly the basics, properties, and some important theorems. The Class 9 Maths NCERT solutions will not only help students to clear their doubts but also prepare more efficiently for the CBSE examination.
NCERT Solutions for Class 9 Maths Chapter 8 – Quadrilaterals
Access Answers to NCERT Class 9 Maths Chapter 8 – Quadrilaterals
Exercise 8.1 Page: 146
1. The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the common ratio between the angles be x.
We know that the sum of the interior angles of the quadrilateral = 360°
Now,
3x+5x+9x+13x = 360°
⇒ 30x = 360°
⇒ x = 12°
, Angles of the quadrilateral are:
3x = 3×12° = 36°
5x = 5×12° = 60°
9x = 9×12° = 108°
13x = 13×12° = 156°

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
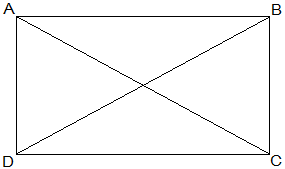
Given that,
AC = BD
To show that ABCD is a rectangle if the diagonals of a parallelogram are equal
To show ABCD is a rectangle, we have to prove that one of its interior angles is right-angled.
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
BC = AD (Opposite sides of a parallelogram are equal)
AC = BD (Given)
Therefore, ΔABC ≅ ΔBAD [SSS congruency]
∠A = ∠B [Corresponding parts of Congruent Triangles]
also,
∠A+∠B = 180° (Sum of the angles on the same side of the transversal)
⇒ 2∠A = 180°
⇒ ∠A = 90° = ∠B
Therefore, ABCD is a rectangle.
Hence Proved.

3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
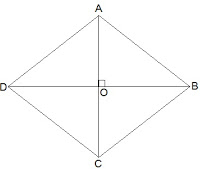
Let ABCD be a quadrilateral whose diagonals bisect each other at right angles.
Given that,
OA = OC
OB = OD
and ∠AOB = ∠BOC = ∠OCD = ∠ODA = 90°
To show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus, we have to prove that ABCD is a parallelogram and AB = BC = CD = AD
Proof,
In ΔAOB and ΔCOB,
OA = OC (Given)
∠AOB = ∠COB (Opposite sides of a parallelogram are equal)
OB = OB (Common)
Therefore, ΔAOB ≅ ΔCOB [SAS congruency]
Thus, AB = BC [CPCT]
Similarly, we can prove,
BC = CD
CD = AD
AD = AB
, AB = BC = CD = AD
Opposite sides of a quadrilateral are equal. Hence, it is a parallelogram.
ABCD is rhombus as it is a parallelogram whose diagonals intersect at a right angle.
Hence Proved.

4. Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
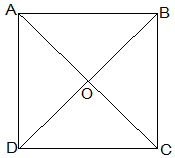
Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show that,
AC = BD
AO = OC
and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
∠ABC = ∠BAD = 90°
BC = AD (Given)
ΔABC ≅ ΔBAD [SAS congruency]
Thus,
AC = BD [CPCT]
diagonals are equal.
Now,
In ΔAOB and ΔCOD,
∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
, ΔAOB ≅ ΔCOD [AAS congruency]
Thus,
AO = CO [CPCT].
, Diagonal bisect each other.
Now,
In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
, ΔAOB ≅ ΔCOB [SSS congruency]
also, ∠AOB = ∠COB
∠AOB+∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90°
, Diagonals bisect each other at right angles
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
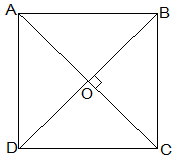
Given that,
Let ABCD be a quadrilateral and its diagonals AC and BD bisect each other at a right angle at O.
To prove that,
The Quadrilateral ABCD is a square.
Proof,
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite)
OB = OD (Diagonals bisect each other)
, ΔAOB ≅ ΔCOD [SAS congruency]
Thus,
AB = CD [CPCT] — (i)
also,
∠OAB = ∠OCD (Alternate interior angles)
⇒ AB || CD
Now,
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Vertically opposite)
OD = OD (Common)
, ΔAOD ≅ ΔCOD [SAS congruency]
Thus,
AD = CD [CPCT] — (ii)
also,
AD = BC and AD = CD
⇒ AD = BC = CD = AB — (ii)
also, ∠ADC = ∠BCD [CPCT]
and ∠ADC+∠BCD = 180° (co-interior angles)
⇒ 2∠ADC = 180°
⇒∠ADC = 90° — (iii)
One of the interior angles is a right angle.
Thus, from (i), (ii) and (iii), given quadrilateral ABCD is a square.
Hence Proved.

6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
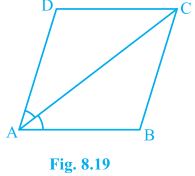
Solution:
(i) In ΔADC and ΔCBA,
AD = CB (Opposite sides of a parallelogram)
DC = BA (Opposite sides of a parallelogram)
AC = CA (Common Side)
, ΔADC ≅ ΔCBA [SSS congruency]
Thus,
∠ACD = ∠CAB by CPCT
and ∠CAB = ∠CAD (Given)
⇒ ∠ACD = ∠BCA
Thus,
AC bisects ∠C also.
(ii) ∠ACD = ∠CAD (Proved above)
⇒ AD = CD (Opposite sides of equal angles of a triangle are equal)
Also, AB = BC = CD = DA (Opposite sides of a parallelogram)
Thus,
ABCD is a rhombus.
7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
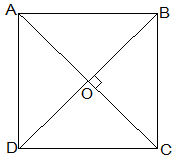
Given that,
ABCD is a rhombus.
AC and BD are its diagonals.
Proof,
AD = CD (Sides of a rhombus)
∠DAC = ∠DCA (Angles opposite of equal sides of a triangle are equal.)
also, AB || CD
⇒∠DAC = ∠BCA (Alternate interior angles)
⇒∠DCA = ∠BCA
, AC bisects ∠C.
Similarly,
We can prove that diagonal AC bisects ∠A.
Following the same method,
We can prove that the diagonal BD bisects ∠B and ∠D.
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Solution:
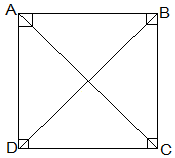
(i) ∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
⇒ AD = CD (Sides opposite to equal angles of a triangle are equal)
also, CD = AB (Opposite sides of a rectangle)
,AB = BC = CD = AD
Thus, ABCD is a square.
(ii) In ΔBCD,
BC = CD
⇒ ∠CDB = ∠CBD (Angles opposite to equal sides are equal)
also, ∠CDB = ∠ABD (Alternate interior angles)
⇒ ∠CBD = ∠ABD
Thus, BD bisects ∠B
Now,
∠CBD = ∠ADB
⇒ ∠CDB = ∠ADB
Thus, BD bisects ∠B as well as ∠D.
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
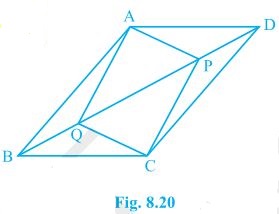
Solution:
(i) In ΔAPD and ΔCQB,
DP = BQ (Given)
∠ADP = ∠CBQ (Alternate interior angles)
AD = BC (Opposite sides of a parallelogram)
Thus, ΔAPD ≅ ΔCQB [SAS congruency]
(ii) AP = CQ by CPCT as ΔAPD ≅ ΔCQB.
(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]
(v) From the questions (ii) and (iv), it is clear that APCQ has equal opposite sides and also has equal and opposite angles. , APCQ is a parallelogram.

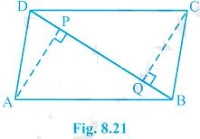
10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
Solution:
(i) In ΔAPB and ΔCQD,
∠ABP = ∠CDQ (Alternate interior angles)
∠APB = ∠CQD (= 90o as AP and CQ are perpendiculars)
AB = CD (ABCD is a parallelogram)
, ΔAPB ≅ ΔCQD [AAS congruency]
(ii) As ΔAPB ≅ ΔCQD.
, AP = CQ [CPCT]

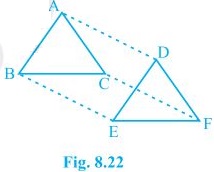
11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see Fig. 8.22).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
Solution:
(i) AB = DE and AB || DE (Given)
Two opposite sides of a quadrilateral are equal and parallel to each other.
Thus, quadrilateral ABED is a parallelogram
(ii) Again BC = EF and BC || EF.
Thus, quadrilateral BEFC is a parallelogram.
(iii) Since ABED and BEFC are parallelograms.
⇒ AD = BE and BE = CF (Opposite sides of a parallelogram are equal)
, AD = CF.
Also, AD || BE and BE || CF (Opposite sides of a parallelogram are parallel)
, AD || CF
(iv) AD and CF are opposite sides of quadrilateral ACFD which are equal and parallel to each other. Thus, it is a parallelogram.
(v) Since ACFD is a parallelogram
AC || DF and AC = DF
(vi) In ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (Opposite sides of a parallelogram)
, ΔABC ≅ ΔDEF [SSS congruency]
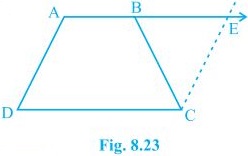
12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Solution:
To Construct: Draw a line through C parallel to DA intersecting AB produced at E.
(i) CE = AD (Opposite sides of a parallelogram)
AD = BC (Given)
, BC = CE
⇒∠CBE = ∠CEB
also,
∠A+∠CBE = 180° (Angles on the same side of transversal and ∠CBE = ∠CEB)
∠B +∠CBE = 180° ( As Linear pair)
⇒∠A = ∠B
(ii) ∠A+∠D = ∠B+∠C = 180° (Angles on the same side of transversal)
⇒∠A+∠D = ∠A+∠C (∠A = ∠B)
⇒∠D = ∠C
(iii) In ΔABC and ΔBAD,
AB = AB (Common)
∠DBA = ∠CBA
AD = BC (Given)
, ΔABC ≅ ΔBAD [SAS congruency]
(iv) Diagonal AC = diagonal BD by CPCT as ΔABC ≅ ΔBAD.

Exercise 8.2 Page: 150
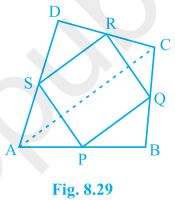
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution:
(i) In ΔDAC,
R is the mid point of DC and S is the mid point of DA.
Thus by mid point theorem, SR || AC and SR = ½ AC
(ii) In ΔBAC,
P is the mid point of AB and Q is the mid point of BC.
Thus by mid point theorem, PQ || AC and PQ = ½ AC
also, SR = ½ AC
, PQ = SR
(iii) SR || AC ———————- from question (i)
and, PQ || AC ———————- from question (ii)
⇒ SR || PQ – from (i) and (ii)
also, PQ = SR
, PQRS is a parallelogram.
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
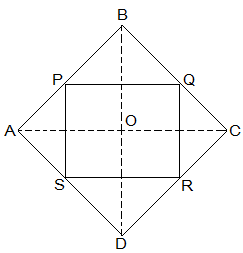
Given in the question,
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
To Prove,
PQRS is a rectangle.
Construction,
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
, ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
, ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC, respectively.
⇒ QR || BD
also,
P and S are the mid points of AD and AB, respectively.
⇒ PS || BD
⇒ QR || PS
, PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
, PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
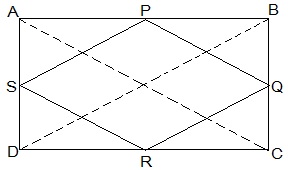
Given in the question,
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively.
Construction,
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
In ΔABC
P and Q are the mid-points of AB and BC, respectively
, PQ || AC and PQ = ½ AC (Midpoint theorem) — (i)
In ΔADC,
SR || AC and SR = ½ AC (Midpoint theorem) — (ii)
So, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.
, PS || QR and PS = QR (Opposite sides of parallelogram) — (iii)
Now,
In ΔBCD,
Q and R are mid points of side BC and CD, respectively.
, QR || BD and QR = ½ BD (Midpoint theorem) — (iv)
AC = BD (Diagonals of a rectangle are equal) — (v)
From equations (i), (ii), (iii), (iv) and (v),
PQ = QR = SR = PS
So, PQRS is a rhombus.
Hence Proved
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
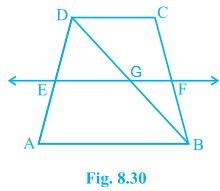
Solution:
Given that,
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove,
F is the mid-point of BC.
Proof,
BD intersected EF at G.
In ΔBAD,
E is the mid point of AD and also EG || AB.
Thus, G is the mid point of BD (Converse of mid point theorem)
Now,
In ΔBDC,
G is the mid point of BD and also GF || AB || DC.
Thus, F is the mid point of BC (Converse of mid point theorem)
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
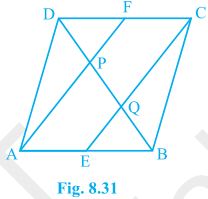
Solution:
Given that,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD, respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒½ AB = ½ CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ — (i)
Similarly,
In ΔAPB,
E is midpoint of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB — (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
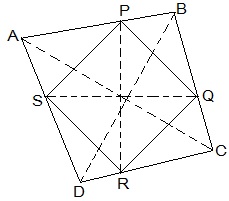
Let ABCD be a quadrilateral and P, Q, R and S the mid points of AB, BC, CD and DA, respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA, respectively.
, SR || AC.
Similarly we can show that,
PQ || AC,
PS || BD and
QR || BD
, PQRS is parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
Solution:
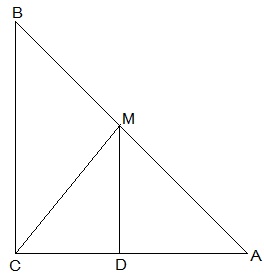
(i) In ΔACB,
M is the midpoint of AB and MD || BC
, D is the midpoint of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
, ΔAMD ≅ ΔCMD [SAS congruency]
AM = CM [CPCT]
also, AM = ½ AB (M is midpoint of AB)
Hence, CM = MA = ½ AB
| Also Access |
| NCERT Exemplar for Class 9 Maths Chapter 8 |
| CBSE Notes for Class 9 Maths Chapter 8 |
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 8 explains the Angle Sum Property of a Quadrilateral, Types of Quadrilaterals and Mid-Point theorem.
Topics covered in this chapter help the students understand the basics of a quadrilateral geometrical figure, its properties and various important theorems. This chapter of NCERT Solutions for Class 9 Maths is extremely crucial as the formulas and theorem results are extensively used in several other maths concepts in higher grades.
Chapter 8 Quadrilaterals is included in the CBSE Syllabus 2023-24 and is a part of Unit – Geometry, which holds 28 marks of weightage in the CBSE Class 9 Maths exams. Two or three questions are asked every year in the board examination from this chapter.
NCERT Solutions For Class 9 Maths Chapter 8 Exercises:
Get detailed solutions for all the questions listed under the below exercises:
Exercise 8.1 Solutions (12 Questions)
Exercise 8.2 Solutions (7 Questions) NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals NCERT Solutions for Class 9 Maths Chapter 8 is about Theorems and properties on Quadrilaterals. They are accompanied with explanatory figures and solved examples, which are explained comprehensively. The main topics covered in this chapter include:
| Exercise | Topic |
| 8.1 | Introduction |
| 8.2 | Angle Sum Property of a Quadrilateral |
| 8.3 | Types of Quadrilaterals |
| 8.4 | Properties of a Parallelogram |
| 8.5 | Another Condition for a Quadrilateral to be a Parallelogram |
| 8.6 | The Mid-point Theorem |
| 8.7 | Summary |
Key Features of NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
- NCERT solutions have been prepared in a logical and simple language.
- Pictorial presentation of all the questions.
- Emphasizes that learning should be activity-based and knowledge-driven.
- The solutions are explained in a well-organised way.
- Step-by-step approach used to solve all NCERT questions.
Disclaimer:
Dropped Topics – 8.1 Introduction, 8.2 Angle sum property of a quadrilateral, 8.3 Types of quadrilaterals and 8.5 Another condition for a Quadrilateral to be a parallelogram.
Frequently Asked Questions on NCERT Solutions for Class 9 Maths Chapter 8
What are the main topics covered in NCERT Solutions for Class 9 Maths Chapter 8?
8.1 Introduction to Quadrilaterals
8.2 Angle Sum Property of a Quadrilateral
8.3 Types of Quadrilaterals
8.4 Properties of a Parallelogram
8.5 Another Condition for a Quadrilateral to be a Parallelogram
8.6 The Mid-point Theorem
8.7 Summary
























This is very good app I love this
It is good for studying